Plano de Aula: Composição e Decomposição de Números
Objetivo:
- Compreender e aplicar os conceitos de composição e decomposição de números, desenvolvendo a habilidade de manipular números de forma eficaz.
Justificativa:
- A composição e decomposição de números são habilidades fundamentais para o desenvolvimento do raciocínio matemático. Ao compreender como os números são formados e podem ser decompostos, os alunos fortalecem sua capacidade de cálculo mental, resolução de problemas e entendimento das relações numéricas.
Conteúdo:
- Composição e decomposição de números no contexto dos números naturais.
Estratégias de Ensino:
Atividade Inicial (10 minutos):
- Realizar uma breve revisão sobre adição e subtração.
- Apresentar exemplos simples de composição e decomposição de números, incentivando a participação ativa dos alunos.
Introdução (15 minutos):
- Explicar o conceito de composição, mostrando como os números podem ser somados para formar um número maior.
- Discutir situações práticas onde a composição de números é aplicada.
Desenvolvimento (30 minutos):
- Dividir a turma em pequenos grupos.
- Propor atividades práticas que envolvam a composição e decomposição de números, como jogos, quebra-cabeças ou problemas do cotidiano.
- Circular pela sala, oferecendo suporte individualizado e estimulando a colaboração entre os grupos.
Discussão em Grupo (15 minutos):
- Promover uma discussão em grupo para compartilhar descobertas e estratégias utilizadas durante as atividades.
- Destacar diferentes maneiras de decompor e compor números.
Aplicação (20 minutos):
- Propor desafios individuais ou em pares que envolvam a composição e decomposição de números.
- Incentivar a resolução utilizando diferentes métodos aprendidos durante a aula.
Avaliação:
- Observação durante as atividades práticas, participação nas discussões em grupo e resolução dos desafios propostos.
- Aplicação de um exercício escrito que envolva a composição e decomposição de números.
- Feedback individualizado para auxiliar no desenvolvimento contínuo dos alunos.
Recursos:
- Quadro branco e marcadores.
- Materiais manipulativos (se disponíveis).
- Atividades impressas ou fichas para os alunos.
Referências:
- Base Nacional Comum Curricular (BNCC) - Matemática para o 4º e 5º ano.
Este plano de aula visa promover uma abordagem prática e participativa, permitindo que os alunos desenvolvam suas habilidades matemáticas de maneira significativa.
Sugestão de atividades
1. Decomponha os numerais abaixo conforme o modelo.
a) 152: 100 + 50 + 2
b) 536: _____________
c) 168: _____________
d) 204: _____________
e) 365: _____________
f) 417: _____________
2. Complete as decomposições abaixo utilizando apenas os números do quadro.
a) 312: ________ + ________ + ________
b) 125: ________ + ________ + ________
c) 515: ________ + ________ + ________
3. Para decompor um número, podemos utilizar a soma de diferentes valores. Selecione os números da tabela que podem ser utilizados para decompor o valor em destaque, seguindo o exemplo.
4. Maria escreveu o seguinte número na lousa.
5 centenas + 2 dezenas + 9 unidades
A composição desse número é:
a) 529.
b) 5029.
c) 5209.
d) 5290.
5. Componha os numerais abaixo.
6. Complete a tabela abaixo com a composição dos numerais e a forma como se lê, seguindo o exemplo.
7. Complete com atenção.
8. Em uma aula de matemática, a professora de Rafaela pediu que ela fizesse a composição do seguinte numeral:
8 centenas + 5 dezenas + 6 unidades
Marque a opção que apresenta a composição correta feita por Rafaela.
a) 8560.
b) 850.
c) 8056.
d) 856.
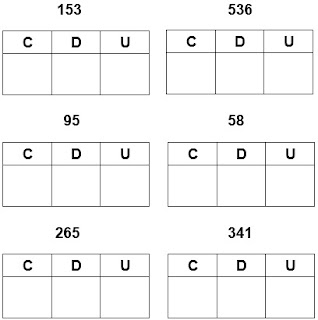
9. Decomponha os números utilizando a tabela abaixo.
10. Leia a composição numérica e represente nas ordens indicadas.
11. Mariane foi a feira e gastou 246 reais com frutas. A decomposição correta do valor que Mariane gastou é
a) 20 + 400 + 6
b) 200 + 4 + 6
c) 200 + 40 + 6
d) 2 + 40 + 600
12. Decomponha os números a seguir.
Fonte: Tudo Sala de Aula
GABARITO
1. b- 500 + 30 + 6; c- 100 + 60 + 8; d- 200 + 4; e- 300 + 60 + 5; f- 400 + 10 + 7. / 2. a- 300 + 10 + 2; b- 100 + 20 + 5; c- 500 + 10 + 5. / 3. Possível resposta: 439- 200 + 200 + 30 + 9; 147- 50 + 50 + 20 + 20 + 7; 315- 200 + 100 + 10 + 5. / 4A / 5. 759, 916, 865, 593. / 6. 16: Dezesseis, 409: Quatrocentos e nove, 32: Trinta e dois, 15: Quinze. / 7. Conferir na questão. / 8D / 9. Conferir na questão. / 10. 09, 05, 25, 13, 49. / 11C / 12. 293: 200 + 90 + 3; 548: 500 + 40 + 8; 434: 400 + 30 + 4; 785: 700 + 80 + 5; 592: 500 + 90 + 2.